航空宇宙工学を専攻する東大院生が,軌道力学の要点・エッセンスをご紹介するシリーズの第2弾! 軌道力学を学び始めた方にとって,専門書はハードルが高いですよね・・筆者がこれまで実際に学習した中でここは!という要点をギュッと詰めました.サクッと,でもきちんと学びたい方必見です.
さて今回は第2弾です.
第1弾はこちら.
二体問題においては,保存量が存在します.
ひとつは,力学的エネルギー,もうひとつは,角運動量です.
二体問題の支配方程式は以下でした.
![]()
![]() が,中心天体に対する周回天体の位置ベクトル,
が,中心天体に対する周回天体の位置ベクトル,![]() はその大きさすなわち距離です.
はその大きさすなわち距離です.![]() は,中心天体を中心とする重力定数で,中心天体の質量と万有引力定数の積で表されます.地球が中心なら,地心重力定数なんてよんだりします.ちなみに,
は,中心天体を中心とする重力定数で,中心天体の質量と万有引力定数の積で表されます.地球が中心なら,地心重力定数なんてよんだりします.ちなみに,![]() 程度です.
程度です.
さて,この式を用いて,保存量を見つけ出しましょう.
力学的エネルギーの保存
ではまず,天下り的ですが,![]() を,両辺に内積的に掛け算します.
を,両辺に内積的に掛け算します.
![]()
ここで,![]() となることを利用します.
となることを利用します.
(この式が成り立つのは,![]() の微分が,
の微分が,
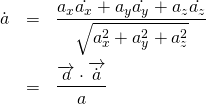
となることより明らかです.)
![]()
このようにかけます.
さらにここで,
![]()
であったことと,
![]()
を考えると,
![]()
を得ます.
さて,![]() としましょう.
としましょう.
上式はつまり,カッコ内が時間変化に対して一定,すなわち定数であることを表しているので,
![]()
となって,これが,力学的エネルギーの保存を表しています.別の流儀では,以下のように書き表すことも多いです.
![]()
角運動量保存
続いて,今度は,![]() を,両辺に外積的に掛け算します.
を,両辺に外積的に掛け算します.
すると
![]()
となります.
同じベクトルの外積は定義上0ベクトルなので,
![]()
となります.
ここで,
![]()
であるから,
![]()
であることがわかります.
これは,位置ベクトルと速度ベクトルの外積の結果生じるベクトル=角運動量ベクトルが,時間変化しないことを表しています.
したがって,角運動量ベクトルが保存することが言えます.
これは,ちょうど高校物理で習う,ケプラーの第二法則,面積速度一定の法則に相当します.
まとめ
今回は,2体の軌道運動で重要な保存則を運動方程式から導出しました.
この導出を理解することにどれほどの価値があるか,と問われると困りますが笑
ベクトルのテクい計算や微積分がいくつか出てきました.ベクトルについては,三次元程度であれば,簡単に成分計算で確認できるので,練習がてら計算してみてください!
微積もこの辺りはすんなり使いこなせないと,やはり,応用工学は苦しいです.数学的な正当性の理解は後回しでも最悪良いので,使いこなせるようにしておきましょう.
次は,ケプラーおじさんが,ニュートンの力学が成立する前から,惑星の運動ってこうなんじゃね?って定式化してたもの=飛行軌道方程式が,やはり正しいんだということをニュートン力学から導いてしまいましょう.



コメント