【流体力学入門】連続の式【第5弾】

航空宇宙工学を専攻する東大院生が，流体力学の要点・エッセンスをご紹介するシリーズの第５弾！ 流体力学を学び始めた学部生や社会人の方にとって，専門書はハードルが高い・・学問では，まず概観をしっかりつかんでおくのが重要だと思っています．筆者がこれまで実際に学習した中でここは！という要点をギュッと詰めました．

 

今回は，連続の式です．

第4弾は，こちら

【流体力学入門】ベルヌーイの式【第4弾】

連続の式とは，流体が連続的に流れる条件を表していて，すなわち流れが可能かどうかということでもあります．

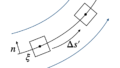
図の検査体積ABCD内に微小時間$\Delta t$に流入する流体の質量は，

$$\rho u \Delta t\Delta y+\rho v \Delta t\Delta x$$

$$= \left(\rho u\Delta y+\rho v \Delta x\right)\Delta t$$

流出するのは，x方向については，

$$\left(\rho  + \frac{\partial \rho}{\partial x}\Delta x\right)\times\left( u + \frac{\partial u}{\partial x}\Delta x\right)\Delta y\Delta t$$

$$=\left[\rho u + \left(\rho \frac{\partial u}{\partial x}+u\frac{\partial \rho}{\partial x}\right)+o(\Delta x^2)\right]\Delta y\Delta t$$

したがって，$\Delta x$が微小なら

$$=\left(\rho u + \frac{\partial (\rho u)}{\partial x}\right)\Delta y\Delta t$$

とできて，y方向も同様に

$$=\left(\rho v + \frac{\partial (\rho v)}{\partial y}\right)\Delta x\Delta t$$

とかける．

また，密度変化による質量変化は，

$$\rho\Delta x\Delta y+\frac{\partial \rho\Delta x\Delta y}{\partial t}\Delta t – \rho\Delta x\Delta y = \frac{\rho}{\partial t}\Delta x\Delta y\Delta t $$

よって，これらのつりあいを考えて，

$$-\left[\frac{\partial (\rho u)}{\partial x}+\frac{\partial (\rho v)}{\partial y}\right]\Delta x\Delta y\Delta t =\frac{\partial\rho}{\partial t}\Delta x\Delta y\Delta t $$

つまり，

$$\frac{\partial (\rho u)}{\partial x}+\frac{\partial (\rho v)}{\partial y}+\frac{\partial\rho}{\partial t}=0$$

を得ます．これこそが，連続の式で，流れている流体はつねにこの条件を満たします．

連続の式はいわば質量保存則です．式そのものを覚えていることも重要ですが，導出から本質を感じていただくことがより重要です．その意味で，これが完全流体ではなく圧縮性流体（こちらも入門シリーズがありますので興味のある方はチェックしてみてください. 【圧縮性流体力学入門】音速とマッハ数【第1弾】

）を対象としていても適用できる（一般性を失っていない）表式だとお分かりいただけると思います．

通常の流体力学では，密度変化を考えることはないため，密度は時間・位置に依存せず，

$$\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}=0$$

と書き直せることがわかります．こちらの方が，馴染み深い書き方ですね．

今回はここまでです．次回は，流れ関数のお話です！