航空宇宙工学を専攻する東大院生が,流体力学の要点・エッセンスをご紹介するシリーズ!
流体力学を学び始めた学部生や社会人の方にとって,いきなり専門書はちょっと・・というケースは多々あるかと思います.学問においては,概観をしっかりつかんでおくのが何より重要だと思っています.筆者がこれまで実際に学習を進めてきた中でここは!という要点をギュッと詰めました.ただし数式はでてきます!笑 サクッとしているがきちんと流体を知りたい方におすすめです.
今回はかの有名なベルヌーイの式です.
第2, 3弾は,こちら
公式だから覚えてしまえ.は悪しき教育の奴隷になってしまっています.こういったシンプルな式は特定の条件下でしか使えません.
それは以下の5つです.
- 非粘性
- 非圧縮
- 定常
- 渦なし
- 物体力が保存力
です.これら全ての仮定が成立するときの流体の運動のエネルギー保存を記述しているのが,ベルヌーイの式であることを念頭においておいてください.
ベルヌーイの式の導出の前に,流体において「加速度」を表現するために重要なことがらについてです.このことは,【流体力学入門】流体粒子の加速度と実質微分【第2弾】でも記載していますので,みてみてください.
加速度とは速度変化の割合のことですが,この速度変化というのは,時間変化と同様に,流れ方向の位置変化によっても生じます.このことを偏微分を用いて記述すると,
$$\Delta V = \frac{\partial V}{\partial t}\Delta t + \frac{\partial V}{\partial s}\Delta s’ $$

これより,
$$\frac{\Delta V}{\Delta t}=\frac{\partial V}{\partial t}+\frac{\Delta s’}{\Delta t}\frac{\partial V}{\partial s}$$
$\Delta t\rightarrow 0$とすると,
$$\frac{DV}{Dt}=\frac{\partial V}{\partial t}+V\frac{\partial V}{\partial s}$$
これが,実質微分と呼ばれるものです.
ちなみに,このあと用いますが,
$$V\frac{dV}{ds}=\frac{d}{ds}\left(\frac{V^2}{2}\right)$$
です.

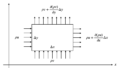
さて,ベルヌーイの式を求めていくわけですが,今回,作用する力として,圧力と重力を考えてみます.すると,上図のように記述できます.今回時間変化による加速度の項は存在しない(作用する力は時間に対して一定)ので,したがって,
$$\rho\Delta s\Delta n\frac{d}{ds}\left(\frac{V^2}{2}\right)=-\frac{\partial p}{\partial s}\Delta s\Delta n -\rho\Delta s\Delta n g\cos\theta$$
$$\rho\frac{d}{ds}\left(\frac{V^2}{2}\right)+\frac{dp}{ds}+\rho g\frac{dz}{ds}=0$$
よって,
$$\frac{V^2}{2}+\int\frac{dp}{\rho}+gz=C$$
非圧縮が前提なので,密度が圧力に対して一定とすれば,
$$\frac{V^2}{2}+\frac{p}{\rho}+gz=C$$
を得ます.これが皆さまご存知の,ベルヌーイの式なんですね!Cは積分定数ですのでどこか一点の情報がすべてわかれば,求められますね.ベルヌーイの式を求めた際に,流線(流れの方向)に対して積分している点がとても重要かなと思います.したがって,流れの中のどの点にあっても,保存する量が存在するということを述べているわけです.そして,第一項の速度の項を見ると分かるように,これはエネルギーの総和をとった式なんです.これが,ベルヌーイの式がエネルギー保存だと言われるゆえんです.
今回はここまでです.次回は,連続の式についてです!


コメント