この分野,非常にニッチなこともあって,意外とネットで気軽に学習ができるようなサイト・ページがありません.
航空宇宙系の院試を受けようとしている方,学部生で軌道力学,宇宙航行力学を学ぼうと考えている人が,本などを見ずとも,さっと学習できるページがあると,便利かなと思いましたので,まとめていきたいと思います!
軌道力学とは
まず,軌道力学とは何なのか.
軌道工学,宇宙航行力学,宇宙軌道力学など様々な呼称がありますが,「軌道力学」は,宇宙飛行体、宇宙機(衛星や探査機)が,天体間を航行する場合の運動を解析する学問のことです.英語では,Orbital mechanics, Astrodynamics, Spaceflight mechanics などと呼びます.
これは「天体力学」から派生したものです.
天体力学は,観察によって,天体(火星や金星ほか小惑星,彗星など)の運動が統一的な物理法則で記述できることを解き明かしました.
惑星等は,いわば力学的な運動法則に従って「受動的な運動を行う飛翔体」ですが,衛星や探査機の登場で,「能動的な運動が可能な飛翔体」が生まれ,その点に関して,より自由度があり,まったく新しい学問が生まれることになりました.
この意味では,軌道力学とするよりも,宇宙航行力学と呼ぶ方がわかりやすいのかもしれませんね.
とはいえ,天体力学を基礎として,新たに加わった宇宙機の航行のための工学を加えて,まとめたものを,「軌道力学」と総称していることが多いです.
重力場における運動方程式:二体問題
ここでは,軌道力学を語る上で,基本中の基本.二体問題と呼ばれるものを扱います.
重要になるのが,万有引力の法則です.
これはさすがにご存知の方が多いと思います.
数学的な話をさせて頂くと,
![]()
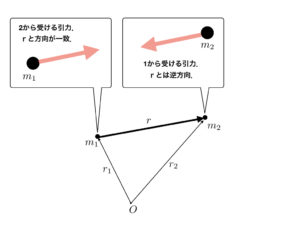
と表されて,![]() は,2物体に働く力(作用・反作用の法則にしたがい,同じ大きさで反対向きの力が働きます).
は,2物体に働く力(作用・反作用の法則にしたがい,同じ大きさで反対向きの力が働きます).![]() は万有引力定数で、
は万有引力定数で、![]() は,2つの物体それぞれの質量,
は,2つの物体それぞれの質量,![]() は2物体間の距離,
は2物体間の距離,![]() はそのベクトルですね(
はそのベクトルですね(![]() を基準にするか,
を基準にするか,![]() を基準にするかで,意味が異なるので注意です).
を基準にするかで,意味が異なるので注意です).
では,今回,質量をそのまま質点の名称に使用させてもらって,![]() から,
から,![]() に向かう方向を
に向かう方向を![]() と定義しましょう.そして,慣性系において,
と定義しましょう.そして,慣性系において,![]() を
を![]() の位置ベクトル,
の位置ベクトル,![]() を
を![]() の位置ベクトルとします.そうすると,
の位置ベクトルとします.そうすると,![]() となります.
となります.
![]()
![]()
両式それぞれ,![]() ,
,![]() で割ることができて,
で割ることができて,
![]()
![]()
この2式から1式を引くと,
![]()
ここで,![]() を
を![]() とおくと
とおくと
![]()
となって,軌道力学でも基本中の基本である二体問題の式を得ます.
![]() は1から2への方向ベクトルであると定義しましたから,この式は,1を基準とする2の運動を表現していることになります.
は1から2への方向ベクトルであると定義しましたから,この式は,1を基準とする2の運動を表現していることになります.
そして,このように考えた場合には,1に対する2の加速度は,1を原点とし,そこに質量![]() がある場合の運動と等価になります.
がある場合の運動と等価になります.
具体的には,1が地球,2が人工衛星というような具合で,この式が適用できて,人工衛星の運動を解析できるわけです.
軌道の形状
数学的には,円錐曲線と呼ばれる形状で軌道は描くことができます.
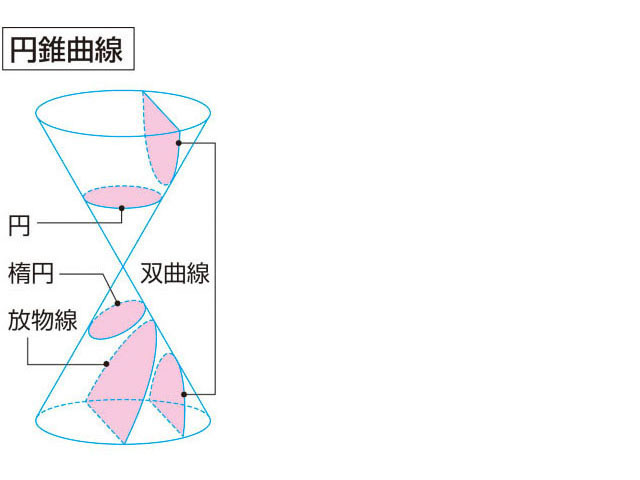
つまり、円、楕円、放物線、双曲線のどれかになるということです。
したがって、これらの数学的な性質やパラメータが、そのまま軌道を決定する重要な要素になります。
そのため、軌道力学の学習では、円錐曲線の基本性質を理解しておくことは大切です。
楕円軌道の基本
宇宙機の軌道のほとんどは,この楕円軌道です.ですので,詳しくみていきましょう.
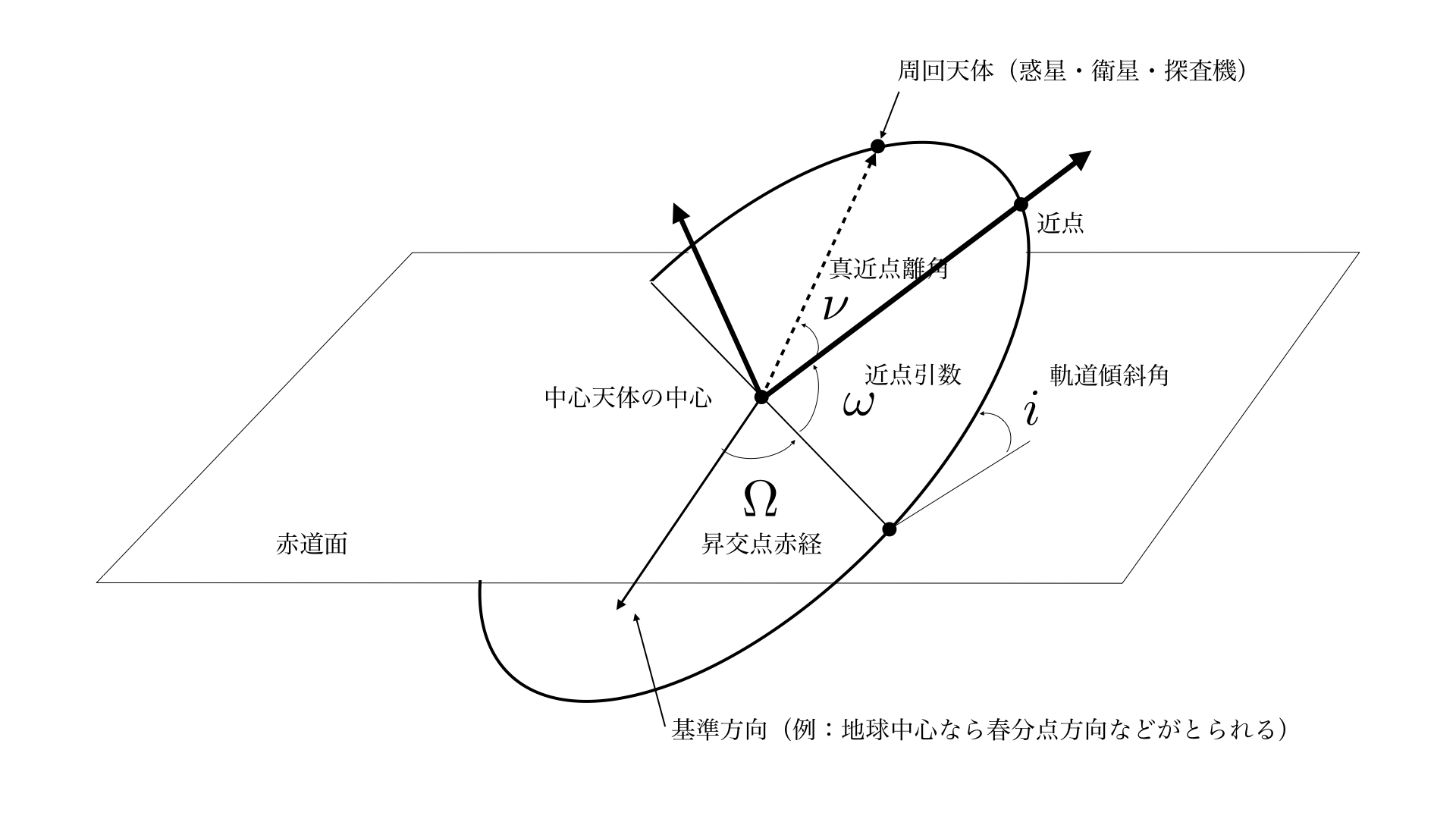
軌道の6要素
ある飛翔体の軌道を決定づけるには,6つの要素を指定してやればいいです.
なぜ6つなのか.それは,3次元の空間座標を考えたとき,位置と速度が決まれば,軌道が一意に決定されることと関係があります.位置情報は3つ.速度情報も3つ.合わせて,6つ.空間上のどの位置にいるかを決めるには,6つの情報が必要になるわけです.上記の表現をカルテシアン表記と呼びますが,この表記は軌道の様子を直感的に理解しづらいです.以下に述べる要素を用いると,視覚的に,直感的に軌道運動を理解できるようになります.
軌道面内の形状を決定する要素
- 軌道長半径(semimajor axis)
一番基本となるパラメータです.軌道そのものの大きさを表します.
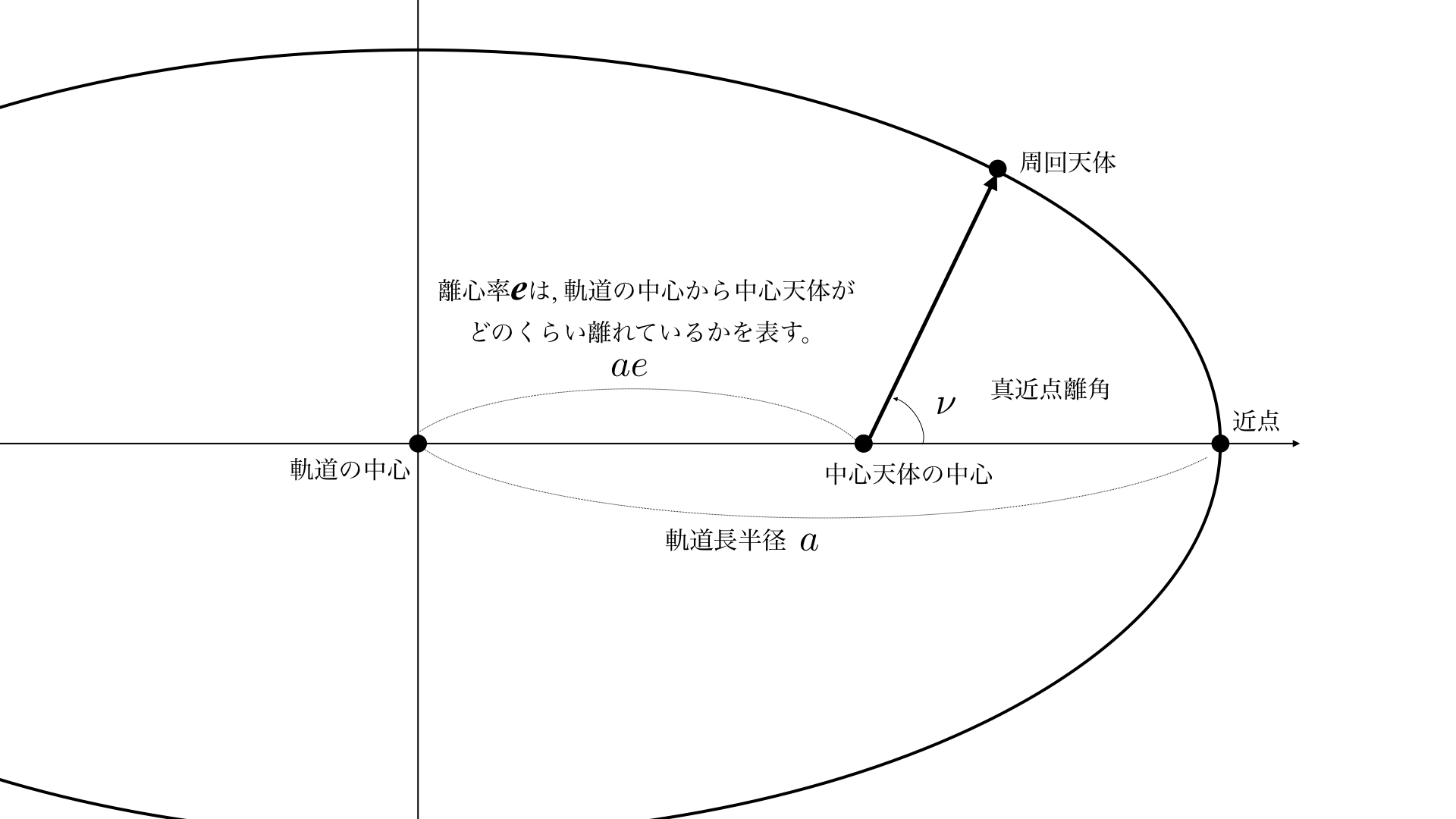
- 離心率(eccentricity)
楕円の中心と,焦点がどの程度離れているかを表現します.こいつが形状を確定するといっても差し支えありません.
- 近地点引数(argument of perigee)
近地点方向が決められた座標の中でどの向きにあるかということを定めます.
軌道面を決定する要素
- 軌道傾斜角(inclination)
決められた空間座標のある面(地球周回の衛星を考える場合には,赤道面などを基準とします)に対して軌道面がどの程度傾いているかを表現します.
- 昇交点赤経(right ascension of ascending node)
ある方向(地球周回軌道を考える場合に典型的なのは,春分点方向)ベクトルと,原点から軌道面が,赤道面と交わる点(昇交点)へ向かうベクトルとがなす角度.昇交点方向の位置を指定する変数です.
軌道上の飛翔体の位置を表す要素
真近点離角(true anomaly)or 平均近点離角(mean anomaly)or 近地点通過時刻(perigee passage time)
要するに,軌道の形が決まれば,あとは,どこにいるかを決めてやればいい.ので,使う情報には,軌道面内で定義される角度を用いるのか,時刻を用いるのかといった自由度があるということになります.そして,どれか一つでよい.なお, 真近点離角(true anomaly)or 平均近点離角(mean anomaly) がどういうものか,相互の関係は何かなどは,今後別の記事で説明したいと思います.
まとめ
軌道力学の基本として,二体の基本運動方程式,円錐曲線と軌道が楕円の場合に定義される軌道要素についてご説明しました.
次回は,二体の方程式から軌道運動に重要な保存量を導出します.



コメント