慣性モーメントってよくわかりませんよね.
僕はしばらく勉強不足で意味も分かっていませんでした.
詰まる人や学ばずにスルーしてしまう人もいるとおもうので,まとめます!
正直まともな力学の教科書を漁れば,書かれているようなことですし,ネット記事すぐに信用してはいけません笑 クロスリファレンス必ずしてください.が,初学者も中にはおられるかと思いますので,教科書では,説明がとばされがちなところや,人に聞かないとわからないような細かい部分もできるだけ説明していきたいと思います.
まず,慣性モーメントという概念を用いるのは,「剛体」を考えるときです.
剛体とは,質点の集まりで,その質点どうしの相対的な距離が,力が加わっても変わらない物体のことです.点ではなく,板や箱などの運動を考え出すと,質点にはなかった自由度(区別しなくてはならない「状態」)が増えます.それが,「姿勢」です.質点の力学で述べられていたのは,物体のグローバルな並進運動であって,物体そのもののローカルな運動についてではありませんでした.むしろ私たちの身の回りにあるのは,質点よりは剛体に近く,それらは姿勢運動を考えることができます.衛星や宇宙機も同様です.グローバルな運動としての軌道.ローカルな運動としての姿勢.宇宙機を設計する場合は当然これら6自由度の運動について考えなければなりません.
さて,そのような剛体が剛体中のある点Oのまわりに角速度![]() で回転している状態を考えてみましょう.剛体は質点の集まりですから,ひとつひとつを
で回転している状態を考えてみましょう.剛体は質点の集まりですから,ひとつひとつを![]() (iは質点の区別のため変わる.たとえば
(iは質点の区別のため変わる.たとえば![]() というように.だが実際は,それら全ての作用を集める.というような記述を行うので,iが何であるかは重要でない)として,その質点の点Oを原点とする位置ベクトルを
というように.だが実際は,それら全ての作用を集める.というような記述を行うので,iが何であるかは重要でない)として,その質点の点Oを原点とする位置ベクトルを![]() , 角速度ベクトルを
, 角速度ベクトルを![]() とします.このとき,質点
とします.このとき,質点![]() の速度ベクトルは,点Oに対して,
の速度ベクトルは,点Oに対して,![]() と
と![]() の外積で表せて,
の外積で表せて,
【注: 使用している数式プラグインでは(というかlatexでは)ギリシャ文字を大文字にできないかつイタリック大文字が使えないので,矢印流儀を採用しています.大文字厨の方がいたらごめんなさい.使えるプラグインを知っている方がいたら教えてください.】
![]()
となります.
ここで,角運動量という物理量を考えます.これは,質量に速度を乗じた量である運動量の,回転モーメント(力のモーメントにはみなさん馴染みがあると思います.その力の部分が運動量に変わったものです)です.
![]()
ここで,ベクトルの計算に対して,
![]()
が成り立つので,(成分計算してみれば正しいことがわかります.)
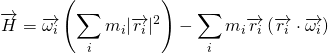
と計算できます.そうすると,
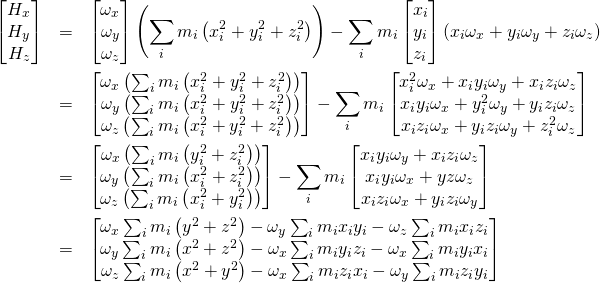
少し胃もたれするくらい丁寧に導出を書きましたが,結果的に,![]() の部分に,角速度の成分が乗じられているという形になっています.そこで,
の部分に,角速度の成分が乗じられているという形になっています.そこで,![]() の部分を以下のように定義します.
の部分を以下のように定義します.
(1) 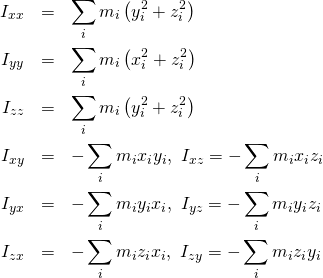
こいつらをつかうと,
先ほどの角運動量の式は,
![]()
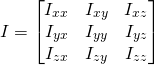
と書けるわけです.
そしてこの角運動量ベクトルは,
質点の運動方程式においても,
![]()
運動量の時間微分が,運動に作用する「力」であると求まるように,
![]()
角運動量の時間微分が,運動に作用する「回転モーメント」=「トルク」であると求まります.
![]()
このようにして,剛体の運動方程式を導く中で生じてきた概念が,慣性モーメントというわけなんですね.
今回はここまで.
次回は,慣性モーメントの計算関連で出てくる定理の整理をしたり,ここで学んだ知識で,宇宙機の姿勢力学・制御なんかも語れたらいいなと思っています!
それでは〜



コメント