複素解析の大事なとこだけ知りたい!概要だけまず捉えたい!という方向けにまとめていきます.ネットでさくっと確認するのに使ってみてください.ちゃんと学ぶ場合は専門書を読んでくださいね.
キーワードをざっとあげちゃうとこんな感じ.ひとつずつ超簡単な説明だけにとどめますが,この辺押さえておけば工学部あたりなら大体だいじょうぶ.
- コーシー・リーマンの関係式
- 調和関数
- 指数関数,三角関数,双曲線関数,対数関数
- オイラーの公式
- 複素積分
- 重要な積分
- 積分評価
- グリーンの定理
- コーシーの積分定理
- 二重連結領域,多重連結領域
- コーシーの積分公式
- テイラー展開(頻出の展開)
- ローラン展開
- 極
- 留数
- 留数定理
- 留数の応用
今回はPart1です!
複素解析って何の役にたつの?
まず,複素解析って何の役に立つのよ,って誰しも思うと思います.答えは
何にでも役に立っている
です.本当にこの方が近いです.例えば,身の回りで言えば,あなたが今使っているそのiPhoneやAndroidなどのスマホは,情報通信技術の結晶なわけですが,その情報通信技術では,電波が鍵を握ることは理解できますよね?また,スマホの中にはもちろんコンピュータがあって,画面を表示するのも音を出力するのもすべて電気信号が大活躍をしています.この電気信号や電波というのは,時間によって周期的な変化をする波なわけです.この波を扱うのに複素数という概念を導入することで,とてつもなく簡単に,それも包括的に表すことができます.この,「とてつもなく簡単に」なったことが,電気や磁気を扱う理論や情報通信技術がここまで発展できた理由なんです.そして,この波ですが,音や光も波の性質を有しているので,音楽を聴いたりカメラで撮影したりできるのも,複素数とその解析論,そしてその応用であるフーリエ解析などのおかげです.つまり,世界が複素数で成り立っているといって差し支えないわけです.なので,何の役に立っているの?はウルトラスーパー愚問なので,これからは,複素数って何にでも役に立っているの?と尋ねるようにしましょう.大学の先生やYouTuberのヨビノリたくみさんなら即答でYEEEEEESと言ってくれることでしょう.
少し遠い例で言えば,中学生の頃は,二次方程式の解で√の中身が負になってしまったら,解は存在しないことになっていましたが,この複素数の概念を取り入れて,存在することとして扱えるようになりました.数学はもちろん物理学など世の中を動かしているもっとも基本的で高尚な言語の中でももっとも重要な「方程式」という概念において,その解が必ず存在するとして扱えるようにすることは,ものすごい威力を発揮してくれます.私たちが日々扱っている電気で動く製品のほとんどが,このものすごい威力ゆえに生まれてきたものです.
このほか,例えば,航空宇宙工学でいえば,
航空機の翼周りの流体の運動を考え,翼がどのように揚力を得て飛ぶのかを考える
衛星がアンテナで受信した天体の電波から画像を生成する
うえでも,この複素解析が役に立ちます.
複素解析の有用性が分かったところで,順番に要点を見ていきましょう!
コーシー・リーマンの関係式
調和関数
指数関数
三角関数
双曲線関数
対数関数
オイラーの公式
複素積分
今回は,複素積分の定義まで来ました.定義は覚えるしかないんで押さえましょう〜!
Part2↓=追記中です.ごめんなさい!!
重要な積分
![]()
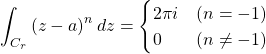
工事中
おわりに
私が複素解析(それ以外も入っちゃってますが・・・)を勉強するのに使っていたものをご紹介しておきます!基本は大学の教科書でいいですが,演習を増やしたい方におすすめしておきます.私が学部の頃なのでもうだいぶ古いですが笑 最近のでよさそうなのがあれば今後追記しておきます.
弱点克服 大学生の複素関数/微分方程式
微分方程式と合わせて基本をおさえつつ自分のものにできるのでおすすめです.具体的には院試の勉強のときに復習用に使っていました!
これならわかる工学部で学ぶ数学
こちらも院試勉強で包括的に復習するために用いたものです.やや難解に感じる人も多いかもしれませんが,一冊にまとまっているメリットは無視できません.あとから知りましたが,著者の千葉逸人先生(Twitter)は非線形力学などで有名な研究者の方です.参考までに!
他の記事ものぞいてみてね.

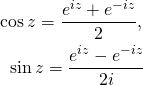
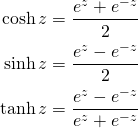
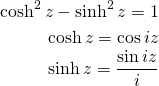
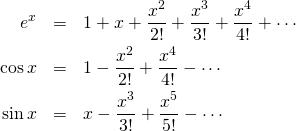
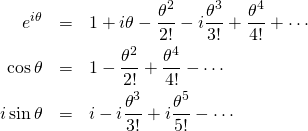


コメント